您所在的位置： 天极下载 > 电脑软件 > 教育教学 > 理科工具 > SplineMaster
SplineMaster

SplineMaster

2.0官方正式版
  • 软件大小：0.22 MB
  • 更新时间：2018-07-05
  • 用户评分：5
  • 软件版本：2.0
  • 软件语言：简体中文
  • 系统类型：支持32/64位
  • 软件授权：免费
  • 下载次数：124次
  • 杀毒检测：无插件360通过金山通过
  • 运行系统：WinAll/Win7

本地纯净下载

纯净官方版
为您推荐： SplineMaster 理科工具

软件简介

　121.jpg　SplineMaster是一款插值计算软件，本程序根据已知散点对未知散点进行插值，插值方法通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

SplineMaster软件特色

　　插值方法通过函数在有限个点处的取值状况

　　估算出函数在其他点处的近似值

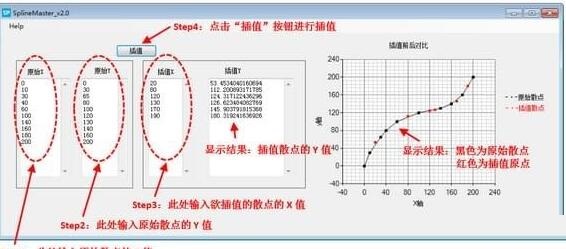
SplineMaster官方电脑端使用方法

　　【什么是插值方法】

　　插值方法通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

　　例如，x和y之间存在某一未知的函数关系，函数表达式不知道，只知道当x=0时，y=0;x=10时，y=30 ;x=30时，y=65 ………..x=200时，y=200。根据这些有限数量的散点，

　　求x等于任意值时，y等于多少?

　　本程序解决的就是这样的问题。数学上的插值方法有很多，本程序采用的是应用最广泛的三次样条插值方法。

　　【本程序使用方法举例】

　　例如， x和y之间存在某一未知的函数关系，函数表达式不知道，只知道十组散点。即，当x=0时，y=0 ;x=10时，y=30 ; x=30时，y=65 ; x=40时，y=80 ; x=60时，y=100; x=100时，y=120 ; x=140时，y=130 ; x=160时，y=140 ; x=180时，y=160 ;x=200时，y=200。

　　根据这已知的十组散点，求当x=20时，y等于多少?X分别等于80、120、130、170、190时，y分别等于多少?

　　求解上述问题，使用本程序，在“原始x”一列中输入已知十组散点的x值，在“原始y”一列中输入已知十组散点的y值，在“插值x”一列中欲求取的散点的x值。输入完成后，点击“插值”按钮，欲求取的y值即显示在“插值y”一列中。

　　如果所用程序是SplineMaster_v2.0，点击“插值”按钮后，在程序界面右侧将绘制出原始散点和插值散点的曲线，用于直观比较插值散点偏离原始散点的程度，防止出现奇异解。曲线中，黑色曲线为原始散点曲线，红色散点为插值得到的散点。

小编寄语

　　【程序版本说明】

　　本程序目前有两个版本， SplineMaster_v1.0和SplineMaster_v2.0，供不同系统使用。

　　SplineMaster_v2.0为最新版本，具有绘制曲线比较的功能，可在windows8或更高版本的操作系统直接使用，在Windows7操作系统使用需安装Microsoft .net framework 4.0(或更高版本)软件

　　SplineMaster_v1.0版本可在windows7、windows8或更高版本的操作系统直接使用，但是该版本没有绘制曲线比较的功能。

软件图集

更多软件图集介绍

提示：软件图集是通过SplineMaster官网或软件客户端截图获取，主要用于分享软件价值，如有侵权请联系我们！

下载地址

夸克浏览器
  • 热门下载
  • 热门分类
  • 热门合集

猜你喜欢

AI桌面浏览器

热门推荐

装机必备

  • SplineMaster截图1
  • SplineMaster截图2

SplineMaster SplineMaster  v2.0官方正式版
关闭

您可能还需要

大家都在玩